Unit Circle and its Relationship with Trigonometry Ratios

In mathematics, a unit circle can be explained as a circle that has a radius of one unit. We know very well that the circle is a two-dimensional geometrical figure which lacks any angles or any sides. Since the unit circle is a subset of circles, the equation of a unit circle is derived with the example of the equation of the circle itself. It also has all the properties similar to that of a circle. The concept of the unit circle and the concept of trigonometry functions have a close relationship with each other. In this article, we will learn the relationship between the unit circle and the trigonometric functions. We will also learn the equation of a unit circle and solve an example related to the concept.

Relationship between Unit Circle and Trigonometry Ratios

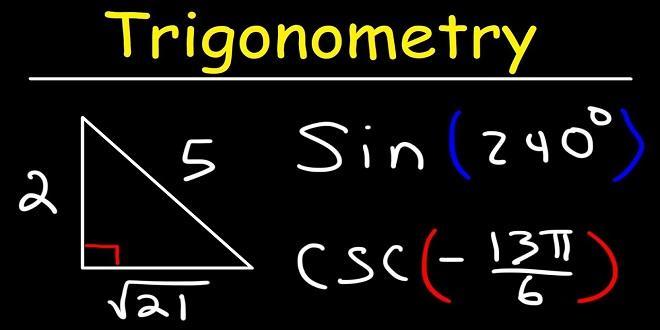
The concept of the unit circle has many applications. One such application is that it is useful in finding out the values of the basic trigonometry ratios i.e. sine, cosine, and the tangent. With the help of these trigonometry ratios, we can then find out the values of cotangent, secant, and cosecant. This process takes the help of the Pythagoras theorem. In the cartesian coordinate plane, we draw a unit circle and in that unit circle, we apply the famous formula of Pythagoras to obtain the values of sine, cosine, and tangent. Many other important trigonometry identities can also be proved easily with the help of the concept of the unit circle.

Equation of a Unit Circle

We know that the standard equation of a circle can be given as (x – a) (x – a) + (y – b) (y – b) = r.r where a and b signifies the center of the given circle and r signifies the radius of the given circle. Using this equation of a circle, we can easily obtain the equation of a unit circle. An important thing to note about a unit circle is that it is formed with its center on the point (0, 0) of the cartesian plane. Also, it has a radius of the measurement of one unit. Substituting these values in the equation of a circle, we get x.x + y.y = 1 which is the required standard equation of a unit circle.

Solved Example of Unit Circle

Example 1: Find out if the point Q (1/4, 1/4) lies on the unit circle.

Solution: We have learned above that the equation of a unit circle is given as:

x.x + y.y = 1.

Now, by substituting the values of 1/4 in x and 1/4 in y of the given equation, we get:

= xx. + y.y = (1/4) (1/4) + (1/4) (1/4) = 1/16 + 1/16 = 2/16 = 1/8.

Now, 1/8 is not equal to 1.

By substituting the values, we see that the given values do not satisfy the general equation of a unit circle. Thus, the point Q (1/4, 1/4) does not lie on the unit circle.

Take Cuemath Classes Online and Become a Math Champion

Do you find math very confusing and difficult? If you do, Cuemath should be your one-stop solution. Their classes are conducted by the best teachers of the subject who go through several interviews and tests before they start teaching on the platform. This helps in ensuring that students who are learning on the platform are getting an education from expert teachers. The primary emphasis of the teachers is the conceptual clarity of the students. Cuemath classes are different from other classes as it teaches students math as a life skill and not just as a school subject. Recreational activities like math puzzles, math games, etc are conducted so that students start finding interest in the subject of math. Experience learning math the Cuemath way by enrolling in a class.